Segunda lei de Ohm
Segunda lei de Ohm
Segunda lei de Ohm estabelece que a resistência elétrica é relacionada a fatores microscópicos e macroscópicos, como a resistividade e a dimensão de área dos condutores.
A segunda lei de Ohm descreve quais grandezas físicas relacionam-se com a resistência elétrica de um condutor. De acordo com essa lei, a resistência elétrica de um condutor homogêneo é diretamente proporcional ao seu comprimento e inversamente proporcional à área transversal desse condutor.
"Fórmula da 2ª lei de Ohm
A segunda lei de Ohm mostra que a resistência de um condutor é relacionada à sua forma mas também a fatores microscópicos, descritos com base em uma grandeza física chamada resistividade.
A resistividade é a grandeza física que mede a oposição que algum material oferece ao fluxo de cargas elétricas, ou seja, materiais de alta resistividade oferecem grande resistência à passagem de corrente elétrica.
A fórmula de segunda lei de Ohm é mostrada a seguir, observe:
R – Resistência (Ω)
ρ – Resistividade (Ω.m)
l – Comprimento (m)
A – Área transversal (m²"
"De acordo com essa fórmula, a resistência elétrica de um fio condutor é diretamente proporcional ao seu comprimento, além disso, é inversamente proporcional à área de sua secção transversal (chamada coloquialmente de bitola). É por esse motivo que utilizamos fios mais grossos em aplicações que demandem correntes elétricas de grande intensidade — eles têm menor resistência elétrica e, por esse motivo, dissipam menos energia em forma de calor."
"Resistividade
A segunda lei de Ohm indica que a resistência elétrica é uma propriedade do corpo, uma vez que essa característica depende diretamente de medidas espaciais, como a área transversal ou o comprimento do corpo.
A resistividade (ρ) é uma grandeza física escalar (medida em Ω.m) que não depende das dimensões do corpo, mas sim de propriedades microscópicas, como a quantidade de elétrons de condução do material e também a distância que esses elétrons conseguem percorrer sem se colidirem com os átomos que compõem o material.
Primeira lei de Ohm
De acordo com a primeira lei de Ohm, a razão entre potencial elétrico e corrente elétrica é sempre constante em resistores ôhmicos, como mostrado na fórmula seguinte:
U – tensão elétrica ou diferença de potencial (V)
R – resistência elétrica (Ω)
i – corrente elétrica (A)
De acordo com a fórmula, a resistência elétrica é a medida relacionada à corrente formada mediante a aplicação de um potencial elétrico: quanto maior for a resistência elétrica de um material, maior será o potencial elétrico necessário para que ocorra o estabelecimento de uma corrente elétrica"
Exercícios resolvidos sobre a segunda lei de Ohm
Questão 1) Determine a resistência elétrica de um fio condutor de 20 metros de comprimento, com área transversal de 8 mm² e resistividade igual a 1,7.10-8 Ω.m.
a) 625 Ω
b) 4,25 Ω
c) 150 Ω
d) 32 Ω
e) 25 Ω
Gabarito: Letra b
Resolução:
Antes de fazermos o cálculo da resistência elétrica, precisamos converter a área transversal do fio, que está em mm², para a unidade de m² (8 mm² = 8.10-6 m²).
Para calcular a resistência desse fio condutor, faremos uso da segunda lei de Ohm, observe:
De acordo com o cálculo, a alternativa correta é a letra b"
"Questão 2) Dispõe-se de um fio condutor de formato cilíndrico, resistência R, resistividade ρ, comprimento L e área transversal A. Mantendo-se fixos os demais parâmetros, qual deve ser a resistência elétrica, escrita em termos de R, de um fio com diâmetro quatro vezes maior?
a) 8R
b) R/4
c) 2R
d) R/16
e) R/8
Gabarito: Letra d"
Resolução:
Como descrito no enunciado, o fio tem formato cilíndrico, isso indica que a área transversal desse fio é de formato circular. A área de uma circunferência, por sua vez, é proporcional ao quadrado do raio (A α r²), portanto, se o segundo fio tem diâmetro quatro vezes maior, seu raio será quatro vezes maior, e sua área transversal, 16 vezes maior.
Uma vez que a área transversal do fio é 16 vezes menor, sua resistência será 16 vezes menor, portanto, a alternativa correta é a letra d."
"Questão 3) Em relação à segunda lei de Ohm, assinale a alternativa correta:
a) A resistência elétrica depende tanto de fatores geométricos quanto de fatores microscópicos.
b) A resistência elétrica não depende de quaisquer fatores macroscópicos, como o comprimento ou a área transversal do condutor.
c) A resistência elétrica é uma grandeza física vetorial medida em Ω.m.
d) A resistência elétrica é diretamente proporcional à área transversal do fio.
e) Resistência e resistividade são grandezas inversamente proporcionais.
Gabarito: Letra a
Resolução:
Vamos fazer a análise das alternativas:
a – VERDADEIRO.
b – FALSO. A resistência elétrica é macroscópica e depende de fatores geométricos, no entanto, depende da resistividade, que é de origem microscópica.
c – FALSO. A resistência elétrica é escalar e sua unidade de medida é somente Ω.
d – FALSO. Resistência elétrica e área transversal são grandezas inversamente proporcionais.
e – FALSO. Resistência e resistividade são grandezas físicas diretamente proporcionais.
Essa lei relaciona propriedades geométricas e uma propriedade intrínseca do material que compõe o corpo condutor: a resistividade. Em termos simples, a Segunda Lei de Ohm estabelece que a resistência de um corpo depende de sua composição e do seu formato: quanto maior for a espessura de um fio, por exemplo, menor será a sua resistência elétrica. Observe o esquema a seguir:
Fórmula da Segunda Lei de Ohm
ρ – resistividade (Ω.m – ohms vezes metro)
l – comprimento do corpo (m – metros)
A – área transversal do corpo (m² – metros quadrados)
A resistividade, representada pela letra ρ, é uma propriedade do material que depende de características microscópicas, como a quantidade de portadores de carga (elétrons, no caso dos metais) disponíveis para condução e o tempo em que essas cargas elétricas são conduzidas no corpo sem colidirem-se com a sua rede cristalina (distribuição espacial de átomos). Além disso, a resistividade é definida como o inverso da condutividade de um corpo.
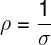
σ – condutividade (Ω-1.m-1 inverso de ohms vezes metro)
Devemos lembrar que, no caso de fios, os quais geralmente apresentam formatos cilíndricos, suas áreas transversais são circulares e podem ser calculadas pela fórmula a seguir:
Tabela de resistividade
A resistividade é uma das grandezas físicas com o maior espectro de valores, podendo variar entre as ordens de grandeza de 10-6 até 1018. A tabela a seguir apresenta os valores de resistividade para alguns materiais conhecidos.
Material
Resistividade (ohms.m.mm2)
Alumínio - 0,029
Antimônio - 0,417
Bronze - 0,067
Chumbo - 0,22
Cobre puro - 0,0162
Constantan - 0,5
Estanho - 0,115
Grafite - 13
Ferro puro - 0,096
Latão - 0,067
Mercúrio - 0,96
Nicromo - 1,1
Níquel - 0,087
Ouro - 0,024
Prata - 0,0158
Tungstêio - 0,055
Zinco - 0,056
A partir da tabela acima, é possível entender a escolha do cobre para
produzir os fios presentes nos postes. Além do baixo custo, esse
metal apresenta um baixo valor de resistividade, diminuindo assim
a quantidade de energia perdida no processo de transmissão de eletricidade.
Níquel - 0,087
Ouro - 0,024
Prata - 0,0158
Tungstêio - 0,055
Zinco - 0,056
A partir da tabela acima, é possível entender a escolha do cobre para
produzir os fios presentes nos postes. Além do baixo custo, esse
metal apresenta um baixo valor de resistividade, diminuindo assim
a quantidade de energia perdida no processo de transmissão de eletricidade.



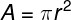


Comentários